Fast Poisson Solver in a Square
The following is a Fast
Solver for the PDE: uxx + uyy = f(x,y) in a square, implemented in Matlab. I
followed the outline from Arieh Iserles' Numerical Analysis of Differential
Equations (Chapter 12), James Demmel's Applied Numerical Linear Algebra (Chapter
6), and some personal inspiration.
This Poisson Solver is written
to use the modified 9-point scheme of order (delta x)^4 instead of the plain
5 and 9 point schemes of order (delta x)^2. However, any of the three schemes
can be used. That is, to call this function, type poisson(m,endpt,N) where m
= the mesh refinement (best to keep below 150 on a PC. m = 150 on my PC took
7-8 minutes to solve), endpt = the endpt of the the square (i.e., 0endpt), and
N = 5,9 or 10. If you want to use the five-point scheme, set N = 5, for the
9-point scheme, set N = 9 and for the Modified 9-point scheme, set N = 10. (If
f(x,y) = 0 in uxx + uyy = f(x,y), it is best to set N = 9 since the 9 and modified
9-point schemes are equivalent when f = 0)
To change the function,
f(x,y), edit ffunc.m
To chenge the boundary conditions, edit Form_Boundary.m.
All of the files below must
reside in the same directory so that they can be called. Poisson.m lists all
necessary files and each file has extensive comments, but the only files that
should be edited are ffunc.m and Form_Boundary.m
Again, to call the function,
type poisson(m,endpt,N), where m,endpt and N are as described above.
- Poisson.m
- The main function which contains calls to subfunctions as well as detailed
descriptions of all files
- Form_Boundary.m
- Stores the Dirichlet boundary condition
- ffunc.m
- Stores f(x,y)
- Form_Right.m
- returns the right-hand side of the problem
- Modified_Right.m
- Called in Form_Right.m if modified 9-point scheme used (N = 10)
- Form_Gamma.m
- Forms the matrix of eigenvalues
- Band_Solve.m
- Finds the band of a Matrix and solves Ax =b,according to A's sparsity and
the does a banded sparse LU decomposition and then passes L, U and b to Back_solve.m
- Back_Solve.m
- Called by Band_Solve.m to do the actual solving. This is actually still
being written. I am rewriting it to pay better attention to the sparse nature
of the L and U matrices passed by the Band_Solve.m function. Currently, it
just uses Matlab's \ (left-divide) routine.
- Transform.m
- Last, but not least, contains the call to the discrete fourier transform,
and implements a fast sine transform by looking only at the imaginary part,
up to a scaling factor. This is used to quickly compute y = Q*b and u = Q*y
where the eigenvector-columns of Q are already known. This works well, but
I am also rewriting this to make it slightly more efficient.
- zipped tarfile - Contains
all of the functions above for quick downloading.
Again, for more information
on each file, look at the head of poisson.m. For more description of the process,
see Iserles' or Demmel's books. Links to the books and their personal websites
are listed below:
Below are several tests
and results of using this program:
Test #1
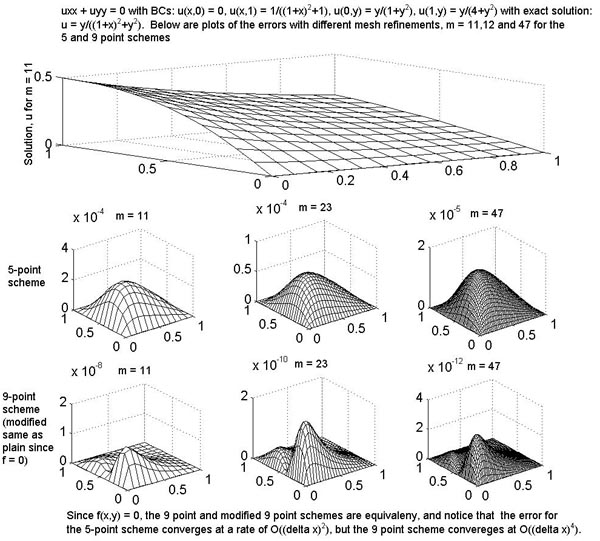
Test #2
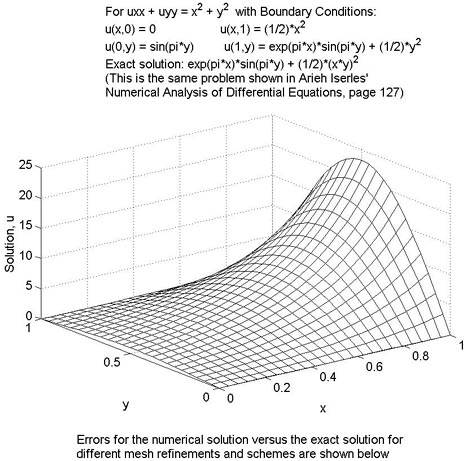
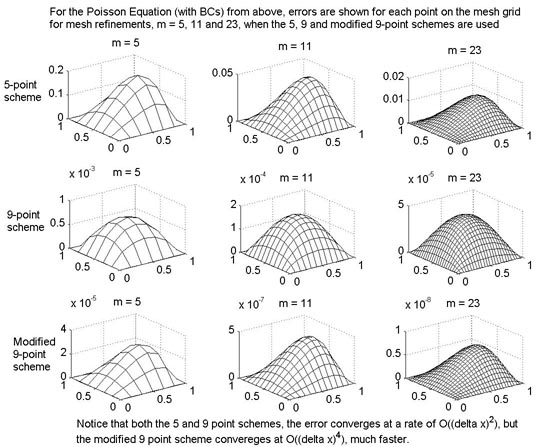
Test #3
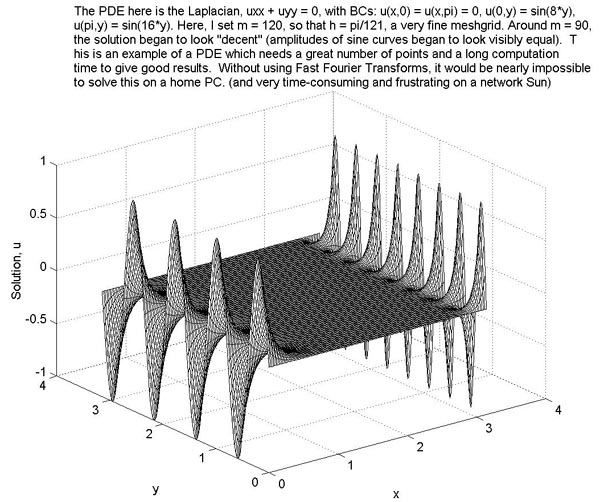
Test #4
( These are currently the
f(x,y) and boundary values stored in ffunc.m and Form_Boundary.m)

Links




